



Fractions are foundational concepts in mathematics, and mastering them is crucial for success in higher-level math. This guide provides a step-by-step approach to learning and understanding elementary fractions, making them less daunting and more enjoyable.
A fraction refers to a part of a whole. Imagine a pizza cut into 8 slices. If you eat 3 slices, you have consumed 3 out of 8 parts, which can be written as the fraction 3/8.
Numerator: The top number (3 in the example) represents the number of parts you have.
Denominator: The bottom number (8 in the example) represents the total number of parts in the whole.
Unit Fraction: The numerator is always 1.
Examples: 1/4, 1/5,1/8...
Proper Fraction
The numerator is smaller than the denominator.
Examples: 1/4, 2/3, 5/6, 3/10...
Improper Fraction
The numerator is the same or bigger than the denominator.
Examples: 6/5, 4/4, 9/6, 15/10...
Mixed Number
When there is a whole number and a fraction as one number, it is a mixed number.
Take a look at the fraction below.

5/4 of the fraction bars shaded.
Also, 1 whole and ¼ of the fraction bars are shaded.
Therefore, we can write 1 whole and 1/4 simply as 1 1/4, and we read it as 1 and 1/4.
This also means that we can convert any improper fraction into a mixed number.
Equivalent Fractions
These are fractions that have the same value. Let’s take a look at the circles below. What fraction of the shape is shaded in each circle?
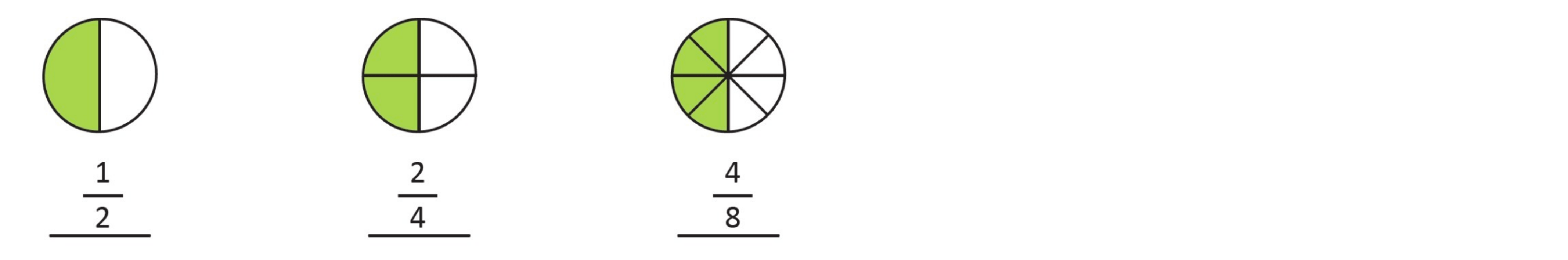
Do the three fractions have the same value? Yes, and the three fractions above are equivalent.
Using Models:
Fraction Bars: Divide a rectangle or bar into equal parts and shade the parts representing the fraction. For example, for 3/8, shade 3 out of 8 equal parts of the bar.

Circles: Divide a circle into equal sectors and shade the sectors representing the fraction.
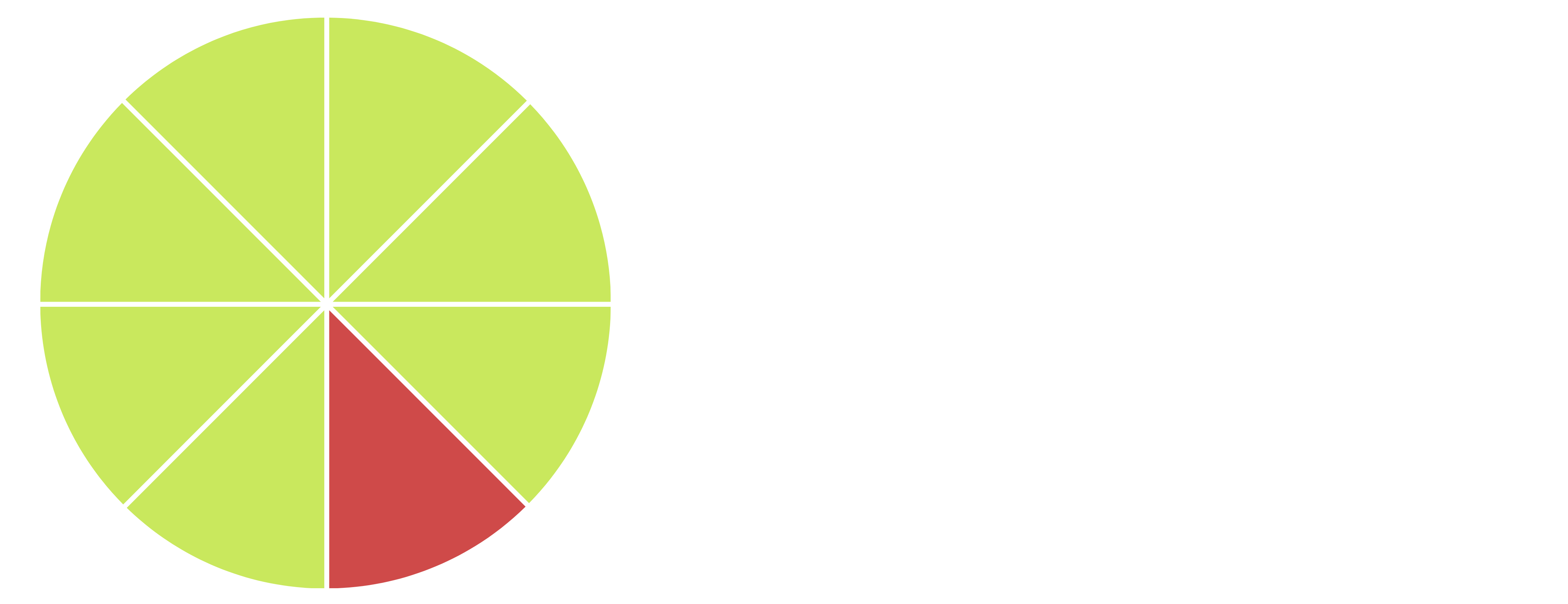
Like Fractions:
Like fractions are fractions that have the same denominator. When adding or subtracting like fractions, simply add or subtract the numerators while keeping the denominator unchanged. For
example, 1/4 + 2/4 = 3/4.
Let’s take a look at the addition of two like fractions below.
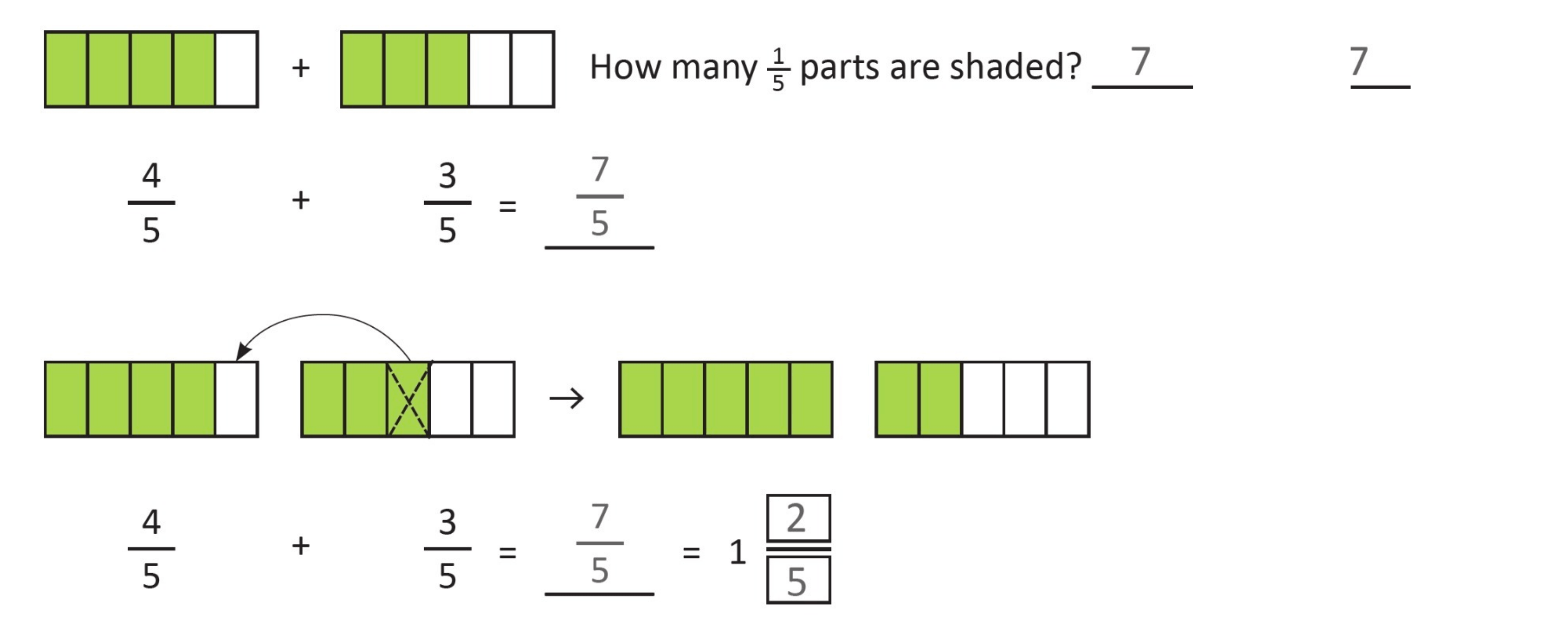
Now, let’s take a look at how we can subtract like fractions.
Suppose Bran had a chocolate bar and ate 3 squares of the bar.

Bran ate 4 more chocolate squares later. What fraction of the chocolate bar did Bran eat?
Correct! It’s 4/12.
How much of the chocolate bar does he have left? Let’s write the subtraction sentence to find the answer.

Bran has 5/12 of the chocolate bar left.
Again, when you subtract two like fractions, you simply subtract the numerator and keep the denominator unchanged.
Let’s dig a bit deeper! How do we add or subtract mixed numbers?
Let’s take a look at the addition of two mixed numbers below.
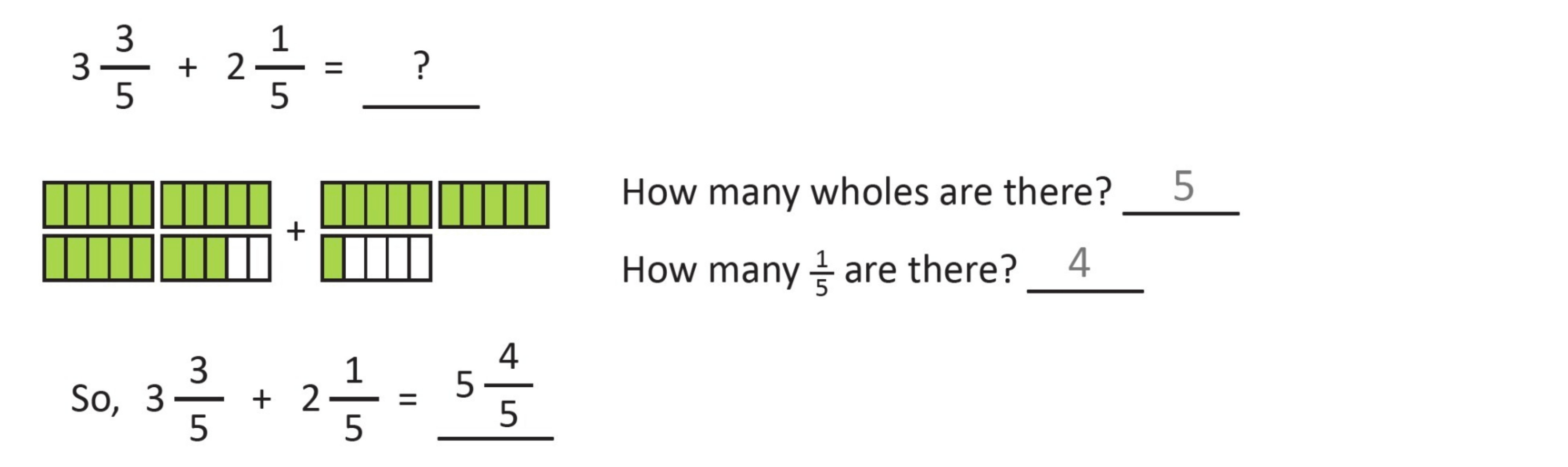
Now, let’s take a look at the subtraction of two mixed numbers below.
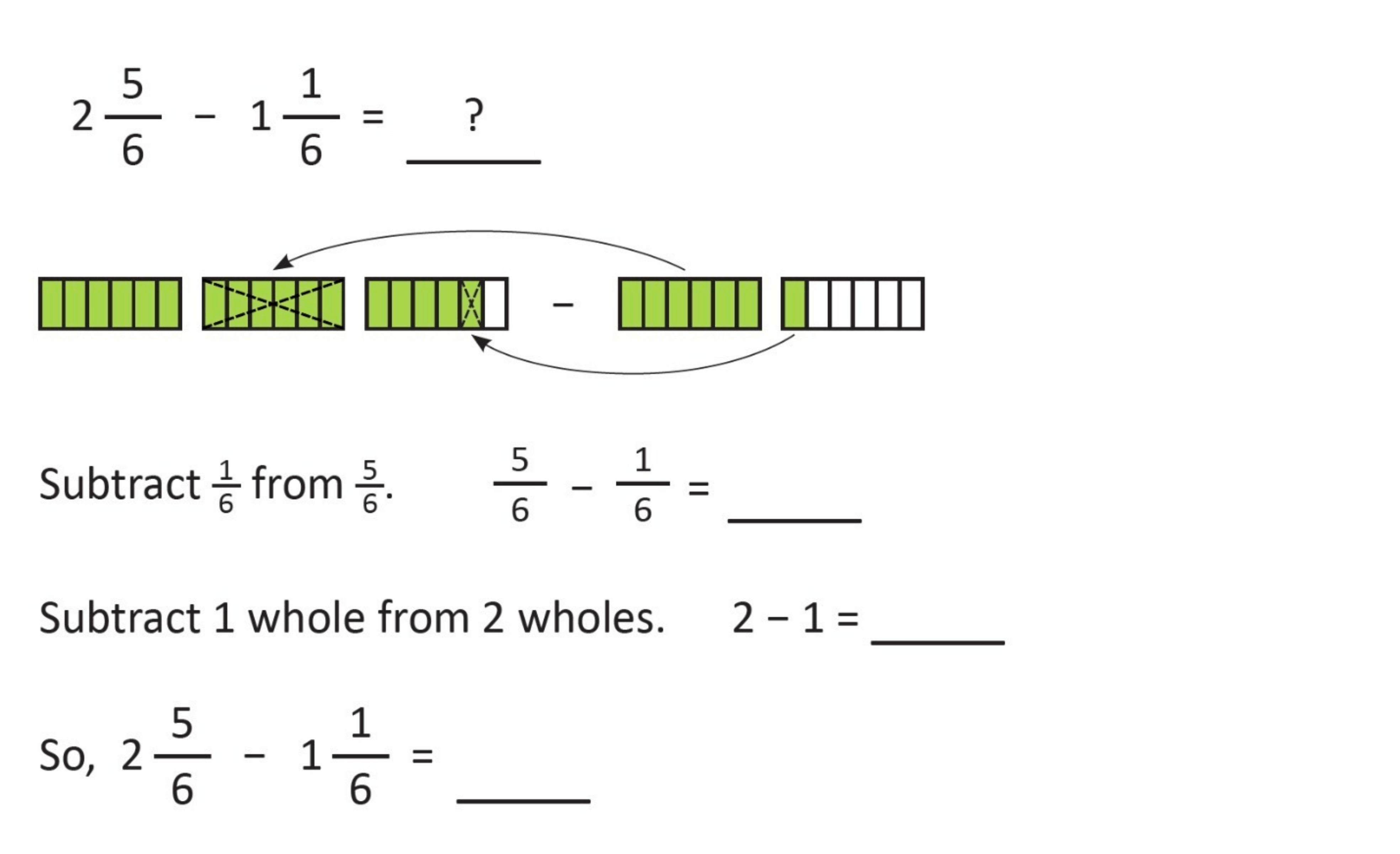
• Solve practice problems regularly to solidify your understanding of fractions.
• Use online resources, games, and apps to make learning more engaging.
• Feel free to seek assistance from teachers, tutors, or classmates without hesitation.
By following these steps and consistently practicing, you can master elementary fractions and build a strong foundation for future mathematical learning. Remember, patience, perseverance, and a positive attitude are key!
Need help with elementary Math? Reach out to the PALS Learning Center today!